1、变频测量原理
干扰十分严重时,变频测量能得到准确可靠的结果。例如用55Hz测量时,测量系统只允许55Hz信号通过,50Hz干扰信号被有效抑制,原因在于测量系统很容易区别不同频率,由下述简单计算可以说明选频测量的效果:
两个频率相差1倍的正弦波叠加到一起,高频的是干扰,幅度为低频的10倍:
Y=1.234sin (x+5.678°) + 12.34sin (2x+87.65°)
在x=0/90/180/270°得到4个测量值Y0=12.4517,Y1= -11.1017,Y2=12.2075,Y3= -13.5576,计算A=Y1 - Y3=2.4559,B=Y0 - Y2=0.2442,则:
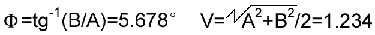
这刚好是低频部分的相位和幅度,干扰被抑制。实际波形的测量点多达数万,计算量很大,结果反映了波形的整体特征。
2、频率和介损的关系
任何有介损的电容器都可以模拟成RC串联和并联两种理想模型:
(1) 并联模型
认为损耗是与电容并连的电阻产生的。这种情况RC两端电压相等:
有功功率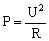
无功功率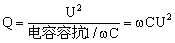
因此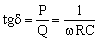
其中ω=2πf,f为电源频率。可见,如果用真正用一个纯电阻和一个纯电容模拟介损的话,它与频率成反比。当R=∞时,没有有功功率,介损为0。
这种方法常用于试验室模拟10%以上的大介损,或用于制做标准介损器。
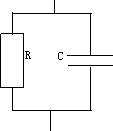
并联模型
(2) 串联模型
认为损耗是与电容串连的电阻产生的。这种情况电路的电流相等:
有功功率
无功功率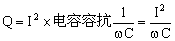
因此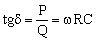

串联模型
由上分析可知,串联模型tgδ=2πfRC,并联模型tgδ=1/(2πfRC),R和C基本不变,f是变化量。把45Hz、50Hz、55Hz分别代入公式,可看到tgδ分别随频率f成正比和反比。如下图所示,f对完全正比和完全反比两种模型影响较大。但实际电容器是多种模型交织的混合模型,此时f的影响就小。
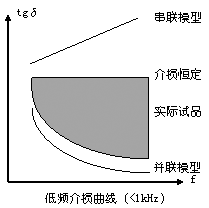
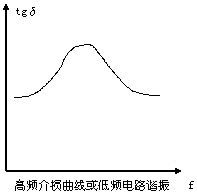
3. 实际电容试品:
(1) 固定频率下测量
实际电容试品在一个固定频率下,即可以用串连模型也可以用并联模型表示。例如50Hz下,下面两个电路对外呈现的特性完全一样:

不同的电桥测量这两个试品,其介损都是31.4%,但西林电桥(2801或QS1)测量的电容量是10000pF,电流比较仪电桥(如QS30)测量的电容量是9101.7pF。这是因为2801电桥认为试品损耗是串连模型,QS30认为试品是并联模型。
通常认为并联模型更接近实际情况,这是因为有功电流穿过电极之间的绝缘层,更象是损耗电阻并联在电极之间,而电极本身电阻为零,没有损耗。
实际上当介损在10%以下时,这种电容量的差别是很小的。
(2) 变频测量
从事现场试验的专家都有这样的经验:使用传统仪器,如QS1,在干扰严重的现场环境下测量介损,采用移相、倒相方法反复测量,仍无法使电桥平衡。
随着电压等级提高,干扰越来越严重。这种情况下变频测量是一个很好的、甚至是唯一的选择。变频测量的抗干扰能力比移相、倒相法提高一个数量级以上。这好比两个电台在同一个频率上,很难将另一个信号抑制掉,但如果两个电台的频率不同,则很容易区分。
4、自动变频与50Hz等效
变频测量受到的唯一怀疑是频率的等效性。按上述模型,介损是随频率变化的。例如50Hz下1%的介损,采用55Hz测量。串联模型的测量结果变成1.1%(正比),并联模型测量结果变成0.91%(反比)。虽然这样的误差可能满足现场测量的要求,但误差还是偏大。
为了解决这个问题,我们首先提出了双变频测量原理:在50Hz对称位置45Hz和55Hz各测量一次,然后将测量数据平均,使误差大大减小。理论分析结果如下表所示:
| 模型 | 50Hz真实介损 | 45Hz测量介损 | 55Hz测量介损 | 平均 |
|---|---|---|---|---|
| 串连 | 1% | 0.9% | 1.1% | 1% |
| 并联 | 1% | 1.111% | 0.909% | 1.010% |
可见最大误差发生在并联模型,相对误差1%。
以上分析表明,采用双变频测量,即发挥了变频测量的高抗干扰能力,理论上的最大相对误差也小于1%,可以满足现场测量需要。也可以采用47.5Hz、52.5Hz双变频测量,理论误差将减少到0.25%,但这时的抗干扰能力肯定不如45Hz、55Hz好。
实际测量显示,变频测量的数据十分稳定,重复性特别好。试验室校验也显示了很好的精度指标。目前变频测量的原理已经得到普遍认可。

